Defining Compound Interest
Compound interest might sound confusing if you’re never heard of it before. It plays a role when we invest, take out loans and save money.
In a nutshell, compound interest is the interest of the interest.
Say that one year you earn 10% interest on a $1,000 investment. Now you have $1,100 and have earned $100 in interest.
The following year, you earn another 10% interest. This time you already have $1,100, so you earn $110 in interest – $10 more than last year.
This is the compounding effect, which Albert Einstein called the 8th wonder of the world.
Compound interest allows you to earn interest on the interest you earned in previous years.
- n
- Compounding interest (or compound interest) is calculated on the initial principal and takes into account all the interest from the loan’s previous periods. n
- Interest can be compounded on different frequencies, such as daily or annually. n
- The number of compounding periods makes a significant difference when calculating compound interest. n
How Compound Interest Works
The way compound interest works are that the interest is added to the principal balance for each term.
This means that interest is then earned on the additional interest added to the original sum over the course of the next compounding period.
You can see an example of how the compound interest effect works on a $1,000 investment below.
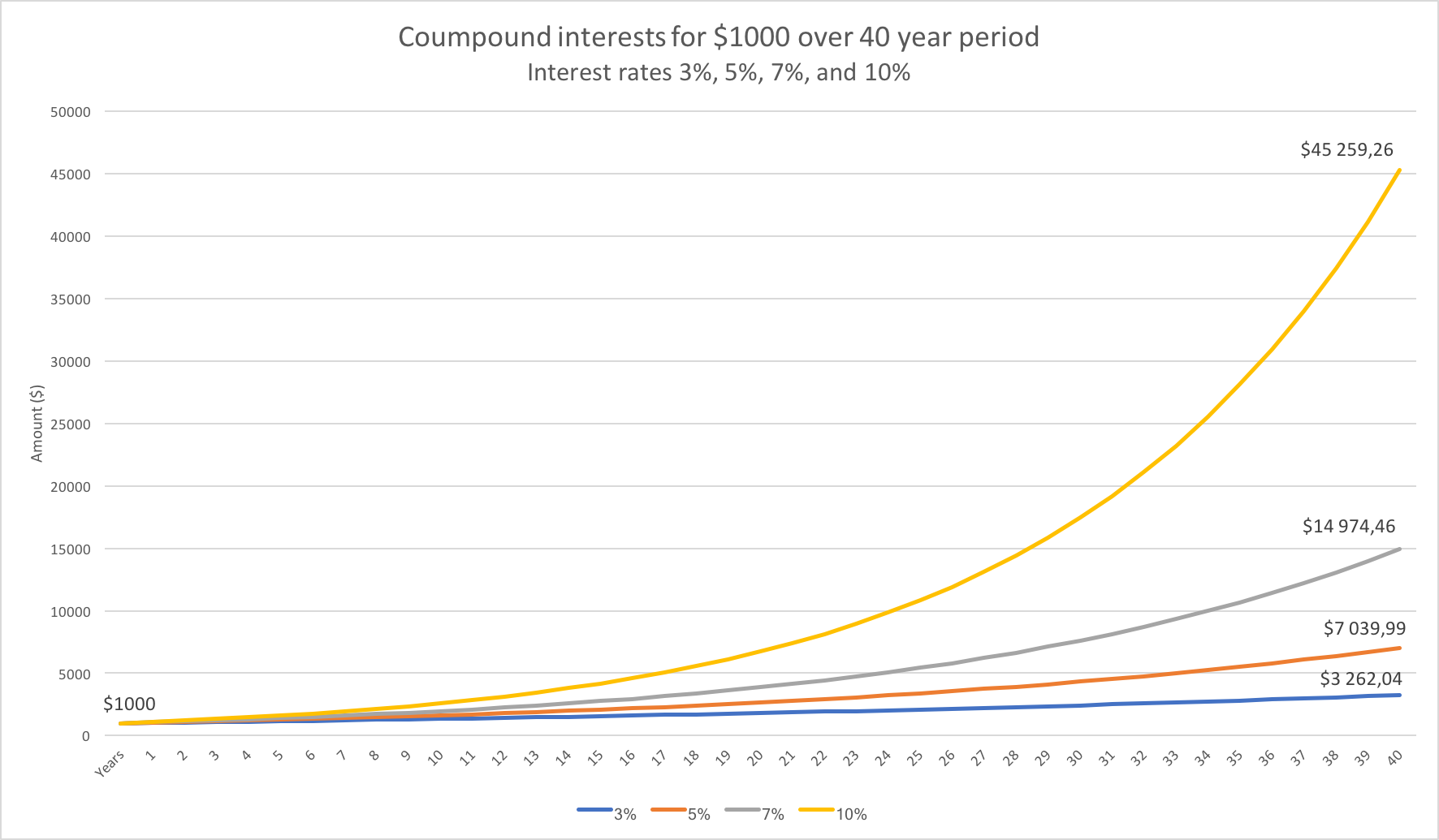
As you can see in the graph, compound interest grows exponentially over the years.
The primary benefit of compound interest is that you can earn interest on the money you never invested, allowing your investments to grow quicker than they could without it.
3 Ways You’re Affected By Compound Interest
- Investing – When you invest your money, you do so with the expectation that your money will grow. The sooner you start investing, the more interest your investment will accumulate.
- Saving – Today, you don’t get much interest on savings accounts, but even small percentages add up in the long run.
- Borrowing – Compound interest can also work against you, for example when you take out a loan. If you don’t pay the loan back on time, the interest will accumulate via the compounding effect, and you will have to pay back more money than originally borrowed.
Annual Compound Interest Formula
The annual compound interest formula is as follows:
A = P (1 + [r / n]) ^ nt
In this case:
A = The future value of the loan or investment, including interest
P = The initial principal amount
r = The annual interest rate
n = The number of times the interest will compound on an annual basis
t = The number of years the money is borrowed or invested
This compound interest equation above will show the future value of an investment or loan, which is the initial principal amount, plus compound interest.
If you want to know how to calculate compound interest only, the formula is as follows:
Total compound interest = P (1 +r/n) (nt) – P
Using the Formula: An Example
Here is an example to show how the compound interest formula works:
If you deposit $1,000 into a savings account with a 5% annual interest rate that’s compounded monthly, then the investment value after five years could be calculated as follows:
P = $1,000
r = 5/100 = 0.05
n = 12
t = 5
A = $1,000 (1 +0.05/12) ^ (12(5)) = $1,283.36
Of course, no one is expected to break out this equation every time you need to figure out compound interest.
Instead, you can use our free compound interest calculator, found at the top of this page for your convenience.
Compound Interest and Credit Cards
If you’ve ever had a credit card you can probably relate to the feeling of being hit with credit card interest charges.
When you try to calculate it, you realize that it’s not that simple – especially since in most cases your interest rate compounds daily.
This simply means that your interest is added to your original (principle) balance at the end of every day.
Generally speaking, your credit card interest rate depends on your creditworthiness. The better your credit rating, the lower your interest rate.
Interest rates are also tied to the prime rate – the interest rates banks charge their biggest customers – so if that goes up, so does your credit card interest rate.
What Does Compound Interest Mean for Investors?
As an investor, you can ensure that compound interest works in your favor.
Start Saving Early
When investing, time is on your side. The longer you invest your money, the more it grows – because of compound interest over time.
For example, if you make a monthly deposit of $100 at 5% interest for a period of five years, you’ll have saved around $6,000 from your deposits over that time, plus earned another $800.61 in interest.
Check the APY
When you compare bank products and investment options, compare the annual percentage yield (APY).
The APY considers compounding to calculate an accurate annual rate. Banks typically make their APY known as it’s usually higher than the interest rate.
Compound Interest FAQs
What’s the difference between daily and monthly compounding?
What is the difference between simple interest and compound interest?
What is the Rule of 72?
In a Nutshell
Compound interest is used in many aspects of business transactions, investments, and financial products.
Make sure compound interest works for you by investing regularly and trying to increase the frequency of your loan payments.
When you know the basics of compound interest you’ll be able to make informed investment decisions and boost your net worth over time.


